Exercise - Directions of $\vec E$ for one charge
- $\vec E$ points away from a positive charge, and toward a negative charge.
Exercise Electric Field
Calculate the magnitude of the electric field given the sepearation between the charge and the observer is $r = [[return sf_latex(namespace_e_field.r_01)]]m$.
$\vec F = q \vec E$.
Since $q_2$ is [[return (~charge_02_charge~>0)? "positive": "negative"]], $\vec F_{21} = q_2 \vec E_1$ tells us $\vec F_{21}$ is [[return (~charge_02_charge~>0)? "parallel": "anti-parallel"]] to $\vec E_1$. Since $\vec E_1$ points [[return namespace_e_field.string_direction_e_field]], we have $\vec F_{21}$ points [[return namespace_e_field.string_direction_e_force]].
Alternatively, we can figure out the direction by observing that the two charges [[return (~charge_01_charge~ * ~charge_02_charge~ >0)? "repel": "attract"]] each other since like charges repel, opposite charges attract.
Calculate $\vec r$, $r$, and $\hat r$.
Draw an arrow $\vec r$ from the charge $q_1$ all the way to the observer. This is the location of the observer from the charge's perspective.
[[return namespace_math_vector.string_explanation_for_component(~~observer_x - ~~charge_01_x, ~~observer_y - ~~charge_01_y, "r", 0)]]
[[return namespace_math_vector.string_explanation_for_magnitude(~~observer_x - ~~charge_01_x, ~~observer_y - ~~charge_01_y, "r", 2)]]
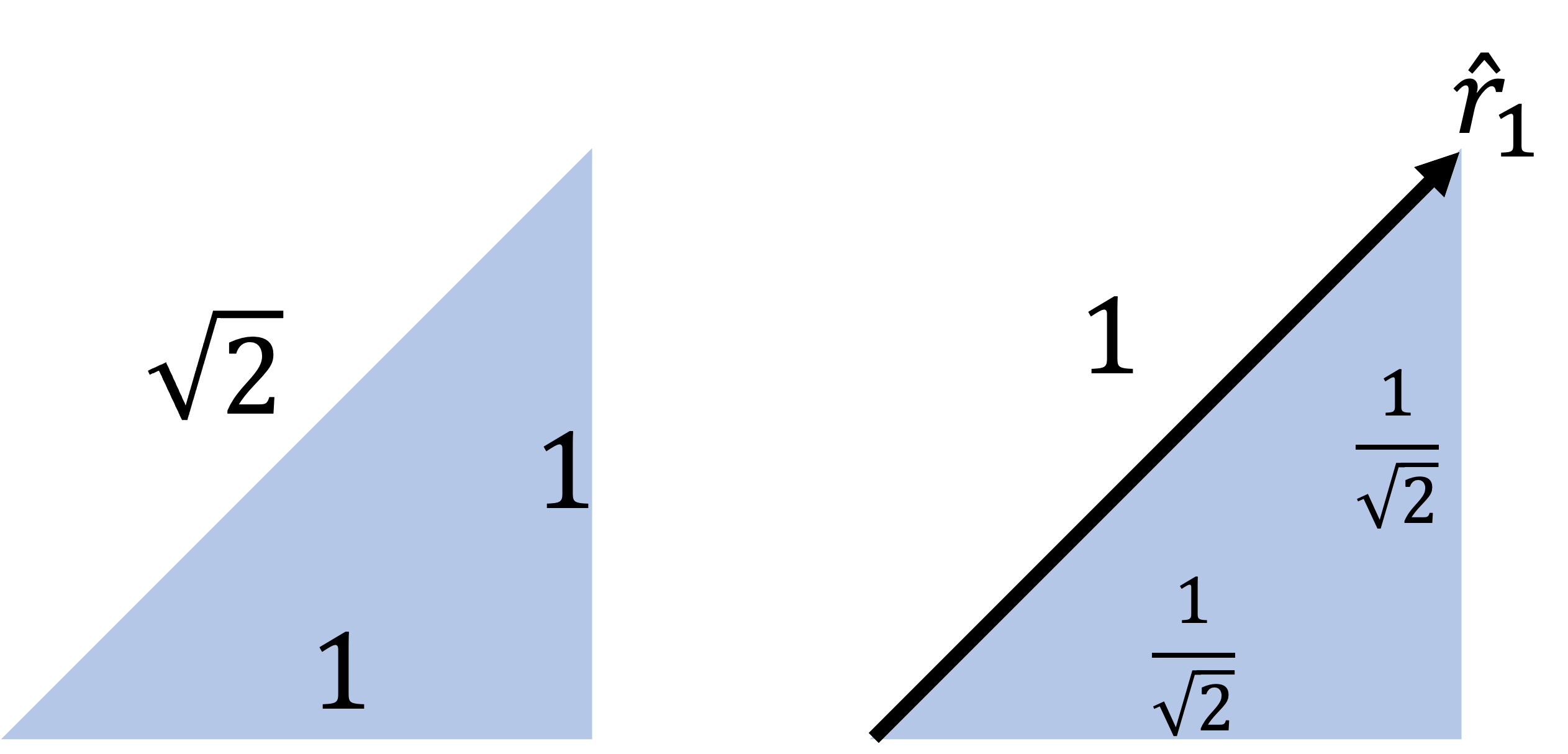
Dividing $\vec r$ by $r=|\vec r|$ then gives: $$ \begin{eqnarray} \hat r &=& \frac{\vec r}{r} \\ &=& \frac{[[return namespace_e_field.r_vector_01.string_mathjax(0, false)]]}{[[return sf_latex(namespace_e_field.r_01)]]} \\ &=& [[return namespace_e_field.r_hat_vector_01.string_mathjax(2, false)]] \end{eqnarray} $$
Calculate the electric field and the related variables below.
It is a long calculation. The key is to do it step by step:
Draw an arrow $\vec r$ from the charge $q_1$ all the way to the observer. This is the location of the observer from the charge's perspective.
[[return namespace_math_vector.string_explanation_for_component(~~observer_x - ~~charge_01_x, ~~observer_y - ~~charge_01_y, "r", 0)]]
[[return namespace_math_vector.string_explanation_for_magnitude(~~observer_x - ~~charge_01_x, ~~observer_y - ~~charge_01_y, "r", 2)]]
Dividing $\vec r$ by $r=|\vec r|$ then gives: $$ \begin{eqnarray} \hat r_1 &=& \frac{\vec r_1}{r_1} \\ &=& \frac{[[return namespace_e_field.r_vector_01.string_latex(2, false)]]}{[[return sf_math(namespace_e_field.r_01)]]} \\ &=& [[return namespace_e_field.r_hat_vector_01.string_mathjax(2, false)]] \end{eqnarray} $$
First we calculate $\frac{q}{4\pi\epsilon_0 r^2} = \frac{k q}{r^2} = \frac{(8.99\times 10^{9})(~~charge_01_charge \times 10^{-9})}{[[return namespace_e_field.r_01.toFixed(2)]]^2} = [[return namespace_e_field.e_with_sign_01.toFixed(2)]]$.
The $x$ and $y$ components of $\vec E$ are then found by multiplying $\frac{q}{4\pi\epsilon_0 r^2}$ and $ \hat r$ (both we just calculated): $$ \begin{eqnarray} \vec E &=& \frac{q}{4\pi\epsilon_0 r^2} \hat r \\ &=& [[return namespace_e_field.e_with_sign_01.toFixed(2)]] ([[return namespace_e_field.r_hat_vector_01.string_mathjax(2, false)]]) \\ &=& ([[return namespace_e_field.e_vector_01.string_mathjax(2, false)]]) N/C \end{eqnarray} $$
Magnitude of the electric field is given by absolute value of the number we just found earlier. Therefore $|\vec E| = |\frac{q}{4\pi\epsilon_0 r^2} | = |[[return namespace_e_field.e_with_sign_01.toFixed(2) ]]| = [[return namespace_e_field.e_magnitude_01.toFixed(2)]] N/C $.
Alternatively: $$ \begin{eqnarray} |\vec E| &=& \sqrt{([[return sf_latex(namespace_e_field.e_vector_01.x)]])^2 + ([[return sf_latex(namespace_e_field.e_vector_01.y)]])^2} \\ &=& [[return sf_latex(namespace_e_field.e_vector_01.magnitude)]] N/C \end{eqnarray} $$It is an even longer problem than the one charge problem! However, most of the steps are exactly the same. The key is to do it one charge at a time:
Draw an arrow $\vec r_1$ from the charge $q_1$ all the way to the observer. This is the location of the observer from the charge's perspective.
[[return namespace_math_vector.string_explanation_for_component(~~observer_x - ~~charge_01_x, ~~observer_y - ~~charge_01_y, "r_1", 0)]]
[[return namespace_math_vector.string_explanation_for_magnitude(~~observer_x - ~~charge_01_x, ~~observer_y - ~~charge_01_y, "r_1", 2)]]
Dividing $\vec r_1$ by $r_1=|\vec r_1|$ then gives: $$ \begin{eqnarray} \hat r_1 &=& \frac{\vec r_1}{r_1} \\ &=& \frac{[[return namespace_e_field.r_vector_01.string_latex(2, false)]]}{[[return sf_math(namespace_e_field.r_01)]]} \\ &=& [[return namespace_e_field.r_hat_vector_01.string_mathjax(2, false)]] \end{eqnarray} $$
First we calculate $\frac{q_1}{4\pi\epsilon_0 r_1^2} = \frac{k q_1}{r_1^2} = \frac{(8.99\times 10^{9})(~~charge_01_charge \times 10^{-9})}{[[return namespace_e_field.r_01.toFixed(2)]]^2} = [[return namespace_e_field.e_with_sign_01.toFixed(2)]]$.
The $x$ and $y$ components of $\vec E_1$ are then found by multiplying $\frac{q_1}{4\pi\epsilon_0 r_1^2}$ and $ \hat r_1$ (both we just calculated): $$ \begin{eqnarray} \vec E_1 &=& \frac{q_1}{4\pi\epsilon_0 r_1^2} \hat r_1 \\ &=& [[return namespace_e_field.e_with_sign_01.toFixed(2)]] ([[return namespace_e_field.r_hat_vector_01.string_mathjax(2, false)]]) \\ &=& ([[return namespace_e_field.e_vector_01.string_mathjax(2, false)]]) N/C \end{eqnarray} $$
Draw an arrow $\vec r_2$ from the charge $q_2$ all the way to the observer. This is the location of the observer from the charge's perspective.
[[return namespace_math_vector.string_explanation_for_component(~~observer_x - ~~charge_02_x, ~~observer_y - ~~charge_02_y, "r_2", 0)]]
[[return namespace_math_vector.string_explanation_for_magnitude(~~observer_x - ~~charge_02_x, ~~observer_y - ~~charge_02_y, "r_2", 2)]]
Dividing $\vec r_2$ by $r_2=|\vec r_2|$ then gives: $$ \begin{eqnarray} \hat r_2 &=& \frac{\vec r_2}{r_2} \\ &=& \frac{[[return namespace_e_field.r_vector_02.string_latex(2, false)]]}{[[return sf_math(namespace_e_field.r_02)]]} \\ &=& [[return namespace_e_field.r_hat_vector_02.string_mathjax(2, false)]] \end{eqnarray} $$
First we calculate $\frac{q_2}{4\pi\epsilon_0 r_2^2} = \frac{k q_2}{r_2^2} = \frac{(8.99\times 10^{9})(~~charge_02_charge \times 10^{-9})}{[[return namespace_e_field.r_02.toFixed(2)]]^2} = [[return namespace_e_field.e_with_sign_02.toFixed(2)]]$.
The $x$ and $y$ components of $\vec E_2$ are then found by multiplying $\frac{q_2}{4\pi\epsilon_0 r_2^2}$ and $ \hat r_2$ (both we just calculated): $$ \begin{eqnarray} \vec E_2 &=& \\ &=& \frac{q_2}{4\pi\epsilon_0 r_2^2} \hat r_2 \\ &=& [[return namespace_e_field.e_with_sign_02.toFixed(2)]] ([[return namespace_e_field.r_hat_vector_02.string_mathjax(2, false)]]) \\ &=& ([[return namespace_e_field.e_vector_02.string_mathjax(2, false)]]) N/C \end{eqnarray} $$
Finally, we add the two electric field vectors together to get the total field: $$ \begin{eqnarray} \vec E_{total} &=& \vec E_1 + \vec E_2 \\ &=& ([[return namespace_e_field.e_vector_01.string_mathjax(2, false)]]) \\ &+& ([[return namespace_e_field.e_vector_02.string_mathjax(2, false)]]) \\ &=& ([[return namespace_e_field.e_vector_total.string_mathjax(2, false)]]) N/C \end{eqnarray} $$
Always remember that $|\vec E_{total}| \neq |\vec E_1| + |\vec E_2|$ in general!