Small Angle Approximation
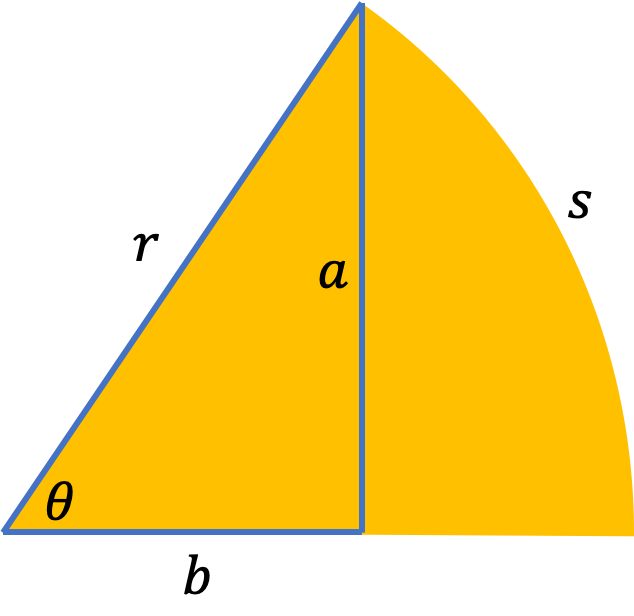
From definition of $\sin$ and $\tan$, we have: $$ \begin{eqnarray} \sin \theta &=& \frac{a}{r} \\ \tan \theta &=& \frac{a}{b} \end{eqnarray} $$ From the definition of radians, we have: $$ \begin{eqnarray} \theta &=& \frac{s}{r} \end{eqnarray} $$

When $\theta$ is small, you could see from the figure $a\approx s$ and $b \approx r$, therefore: $$ \begin{eqnarray} \sin \theta &=& \frac{a}{r} \approx \frac{s}{r} = \theta \\ \tan \theta &=& \frac{a}{b} \approx \frac{s}{r} = \theta \\ \end{eqnarray} $$ Therefore we have the small angle approximation:
Taylor's expansion for small $\theta$ gives: $$ \begin{eqnarray} \sin \theta &\approx& \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} + \cdots &\approx \theta \\ \cos \theta &\approx& 1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} + \cdots &\approx 1 \\ \end{eqnarray} $$ Apply to $\tan \theta$: $$ \begin{eqnarray} \tan \theta &=& \frac{\sin\theta}{\cos\theta} \\ &\approx& \frac{\theta}{1} \\ &\approx& \theta \end{eqnarray} $$
| $\theta$ ($rad$) | $\theta$ ($ ^\circ$) | $\sin \theta$ | $\tan \theta$ |
|---|---|---|---|
| 0.01 | 0.57 | 0.01000 | 0.01000 |
| 0.05 | 2.86 | 0.04998 | 0.05004 |
| 0.1 | 5.73 | 0.09983 | 0.10033 |
| 0.5 | 28.65 | 0.47943 | 0.54630 |
| 1 | 57.30 | 0.84147 | 1.55741 |