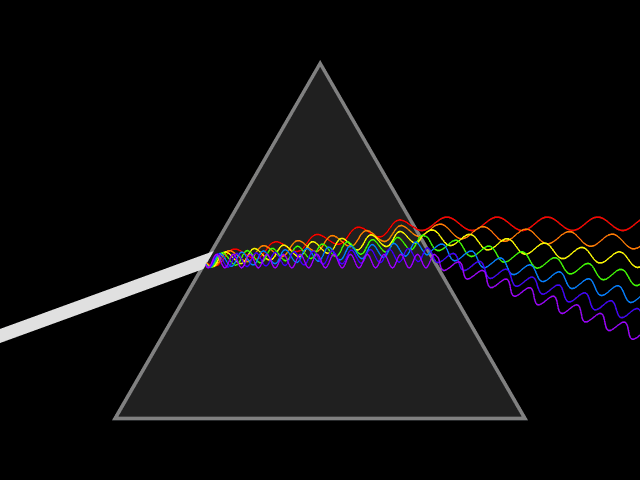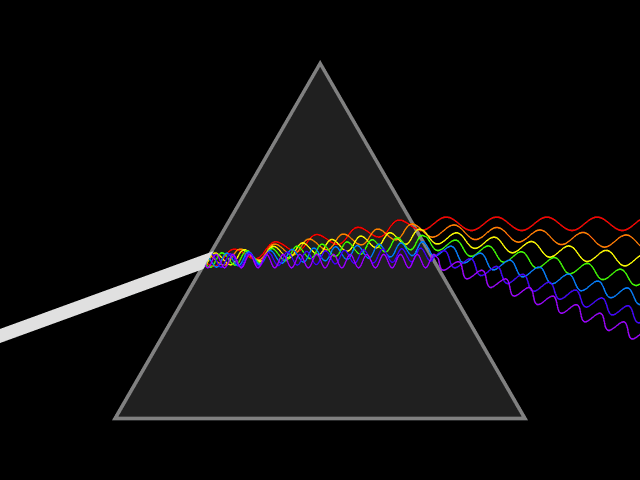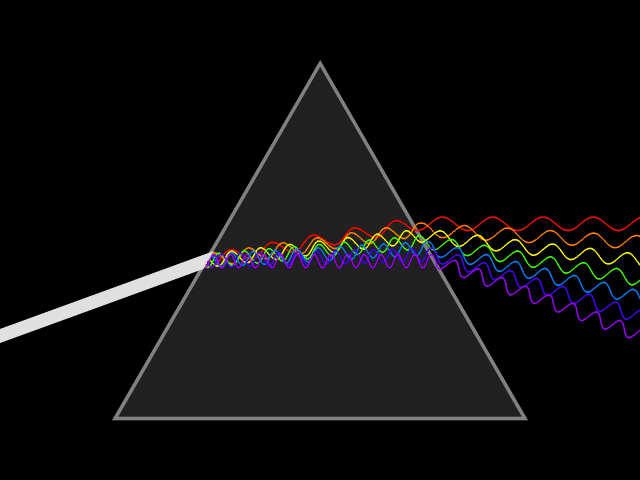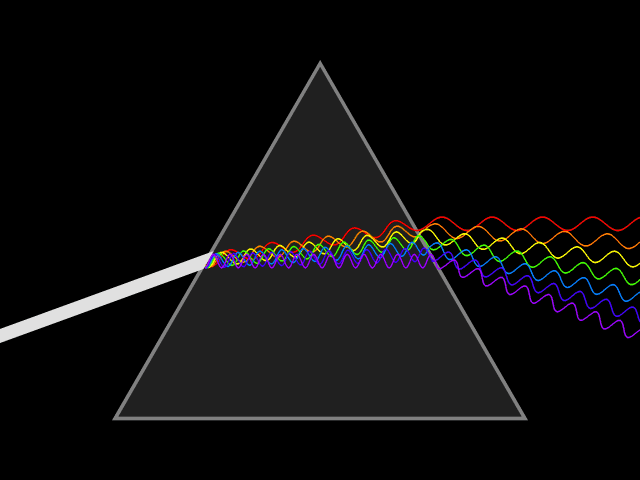
Reflection
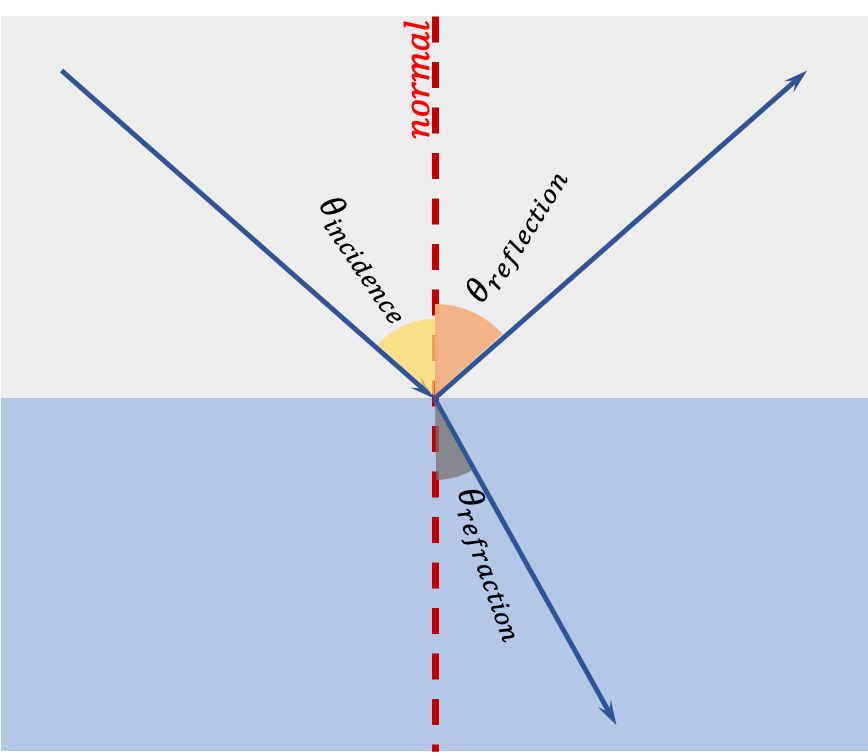
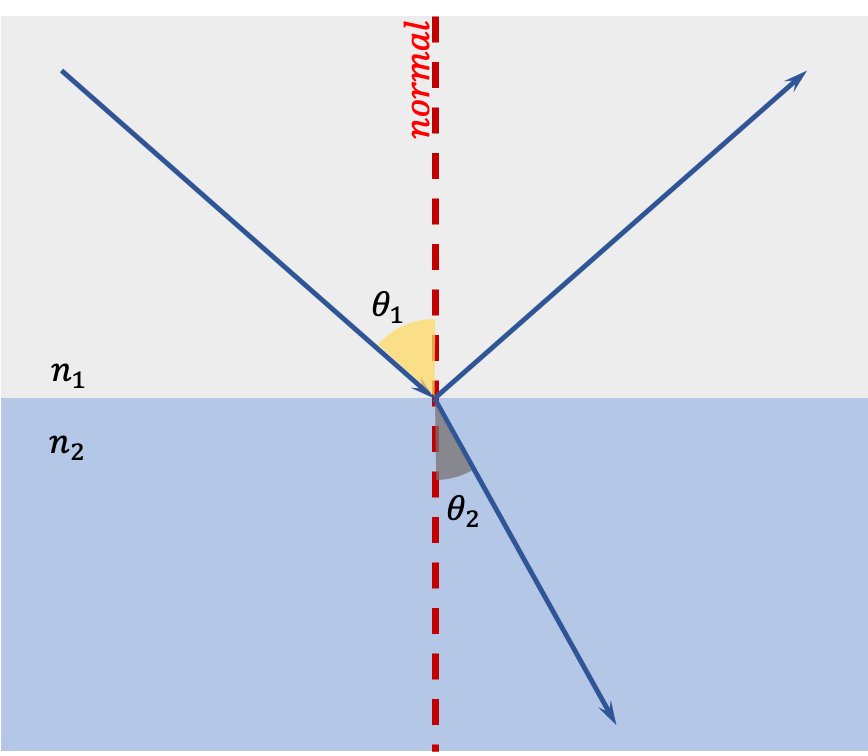
The law of reflection is:
- Normal is a line perpendicular to the boundary between the two media.
- Both the angle of incidence and angle of reflection are measured with respect to the normal.
- The complete law has a little more details but this simplified version is good enough for us.

Image produced by a flat mirror
- Follow any light rays that enter the eyes backward. Wherever the rays meet is the location of the image, where we perceive as the source of light.
- Draw any light rays from the object, use the law of reflection to draw the reflected rays. The reflected rays all lead backward and cross the location of the image. You can try this yourself on a piece of paper.
- The image is as far behind the mirror as the object is in front (object distance = image distance).
- That is why you see a copy of yourself behind the mirror when you brush your teeth in the morning. It is an optical illusion.